
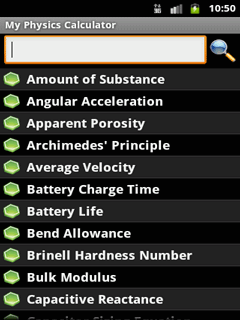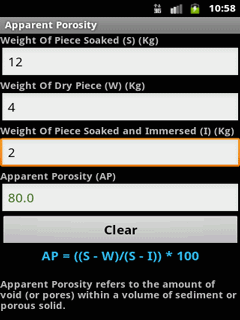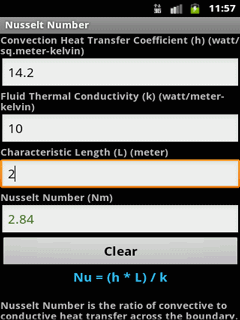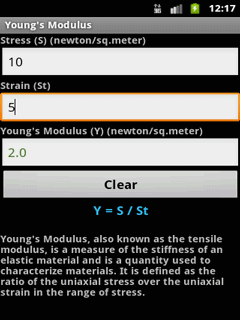
Launching an object from the ground (initial height h = 0) Hmax = h + V² x sin(α)² / (2 x g) Equations for Projectile Motion After reading the above steps for calculating projectile motion, you might feel frazzled! You won’t remember them all, but these below are important: When you launch an object from an initial height (h), you only need to add that value to the final formula: It becomes 0 for a moment in time.Īll you need to do then is find the vertical distance from the ground: The vertical velocity then changes from a positive number to a negative one. Your golfball will reach a point when it reaches its maximum altitude. Time can be entered or solved for in units of secondes (s), minutes (min), hours (hr), or hours and minutes and seconds (hh:mm:ss). The Speed Distance Time Calculator can solve for the unknown sdt value given two known values. What if the initial elevation is not 0? The long formula needs some minor alterations: Calculate speed, distance or time using the formula d st, distance equals speed times time. If you launch a golf ball from the ground (height = 0), the formula will be: The total horizontal distance during travel dictates the projectile’s range. T = / g 4.Ĝalculate the projectile’s range If you are adding elevation to the object, you solve a quadratic equation first. Using that formula, you can establish the time of flight is: You can determine this as being when the vertical distance to the ground is 0. The flight time ends when the projectile hits the ground. Vertical acceleration = -g (gravity acts on a projectile) 3.Ĝalculate the flight time Vertical velocity = Vy – g x t Acceleration - Horizontal acceleration = 0 Vertical distance from the ground is y = h + Vy x t – g (gravity) x t² / 2 Velocity - Horizontal velocity = Vx Distance - Horizontal distance traveled is x = Vx x t (time) If α = 90°, then it’s a freefall.Ģ.Ğstablish the equations of motion. If the vertical velocity is zero, then you have horizontal projectile motion. Three vectors (V, Vx, and Vy) = a right triangle The calculator uses the following steps to work out the remaining parameters for you.ġ.Ĝalculate your velocity components. Once you know the initial velocity ( v), launch angle ( α), and initial height ( h), use the calculator. Analyzing Projectile Motion Projectile motion might look complicated, but it involves logic. If you involved a second force, then it would not be a projectile. In that motion, there is one force: gravity. Anything forming that movement, like an archer shooting an arrow, is projectile motion. It would look like a curve (trajectory) in a parabolic shape. Pay attention to the movements that ball made. It will then start its descent, showing promise for that elusive hole-in-one! The further it moves toward the green, the slower its ascent becomes. Imagine him hitting the ball, blasting it forward and up. What is the Definition of Projectile Motion? For an example of projectile motion, let us look at a golfer. Use a projectile motion calculator to learn about velocity, flight, and projectile ranges. Finally, we comment on a correlation between the parameters of the cosmological magnetic field and the stochastic gravitational wave background coming from the merger of primordial black hole binaries as the primary observable signature of this scenario.Do you want to analyze parabolic projectile motion? What about knowing more about what it means? Do you want to determine projectile motion equation values?īelow, you can learn all this and more. To motivate this scenario, we briefly discuss how new physics may have induced a chemical potential which could have briefly maintained the black holes in an electrically charged state in the early Universe. We find that near-extremal black holes in the mass range M ∼ 10 28 – 10 36 g could potentially generate magnetic fields with present day values as large as B ∼ 10 − 20 – 10 − 15 G those with M ≳ 10 38 g could have produced even larger fields B ≳ 10 − 14 G. To this end, we calculate the strength and correlation length of the magnetic fields generated by this population, and describe their evolution up to the current epoch. In this study, we consider whether these magnetic fields could have been generated in the early Universe by a population of charged, spinning primordial black holes. The origin of our Universe’s cosmological magnetic fields remains a mystery.


 0 kommentar(er)
0 kommentar(er)
